Krumme Statistiken

Thema: Bananen und Prozentrechnung

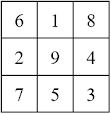
Ich habe Anfang Dezember eine Fortbildung zum Thema "Globale Ernährung" besucht. Dort wurden unter anderem verschiedene Unterrichtsmethoden vorgestellt, die wir auch selbst ausprobieren konnten. Bei einer davon ging es um die Zusammensetzung der Kosten einer handelsüblichen Banane, sprich: welcher prozentuelle Anteil des Verkaufspreises an wen geht:

Das ausgefüllte Arbeitsblatt des Autors. (Bildquelle: Johannes C. Huber)

Gegen Ende der Veranstaltung wurde uns dann die Musterlösung offenbart:

• Löhne: 6,7 %
• Produktion: 6,1 %
  
• Großhandel & Reifereien: 11,4 %
  
• Einzelhandel: 23,9 %
  
• Zoll: 11,8 %
• Import: 23,9 %
  
• Export: 5,5 %

Da mir die Abbildung bekannt vorkam, habe ich im Anschluss ein bisschen recherchiert, welches Datenmaterial als Grundlage verwendet wurde und bin schon nach kurzer Zeit fündig geworden. Die Prozentsätze basieren auf Berechnungen von BASIC (Bureau d'Analyse Sociétale pour une Information Citoyenne) aus dem Jahr 2014 und dazu passende Grafiken gibt es in vielen unterschiedlichen Ausführungen im Internet. Die Wissenschaftsjournalistin Sarah Zierul hat sie beispielsweise für ihr Buch Billig. Billiger. Banane. Wie unsere Supermärkte die Welt verramschen. aus dem Jahr 2015 verwendet:

Eine Abbildung ohne nähere Quellenangabe im oben genannten Buch. (Bildquelle: Johannes C. Huber)

Ich bin mir auch ziemlich sicher, dass ich die zugehörigen Rohdaten ausfindig machen konnte und habe außerdem noch einige weitere Abbildungen analysiert, bei denen ähnliche Aufteilungen vorgenommen werden. Allerdings stammen die neuesten Datensätze höchstens aus dem Jahr 2015. Bei den anderen konnte ich diesbezüglich leider keine Angaben finden. Aber das spielt wahrscheinlich gar keine allzu große Rolle, weil die Prozentsätze in den meisten Fällen mehr oder weniger übereinstimmen.

Bei derartigen Grafiken soll in erster Linie eine Botschaft transportiert werden und in diesem Fall geht es vor allem darum zu betonen, wie ungleich die Verteilung ist. Schließlich kommt jenen Menschen, die tatsächlich für den Anbau und die Ernte zuständig sind, nur ein vergleichsweise geringer Anteil zu. Aus mathematischer Sicht ist allerdings zu kritisieren, dass sich die Stücke einer Banane bzw. ihre zweidimensionalen Flächen nicht für eine derartige Veranschaulichung eignen, weil die Frucht an den Enden schmaler ist, wie im Extremfall an einem Beispiel wie diesem gut ersichtlich sein sollte:

Veranschaulichung nur scheinbar gleich großer Anteile (Bildquelle: abgeändert nach DGB einblick 07/15)

Diese Abbildung stammt aus einem Infoschreiben des deutschen Gewerkschaftsbundes. Vermutlich wurde hier nicht etwa die Fläche, sondern lediglich die Länge der Stücke als Vergleichskriterium herangezogen und selbst das ist nicht einwandfrei gelungen. So sind beispielsweise drei Stücke, die jeweils vier Prozent entsprechen, aneinandergereiht immer noch länger als ein zwölf Prozent-Stück. Das Gleiche gilt auch für die zwanzig Prozent Ganz abgesehen von der Tatsache, dass ihre Flächen nicht einmal ansatzweise jene des vermeintlich gleich großen Stücks abdecken.

Finde die Fehler. (Bildquelle: abgeändert nach Diercke)

Noch absurder wird das bei diesem Beispiel aus einem Schulatlas: Wenn wir ein Stück, das acht Prozent entsprechen soll, in ein anderes hineingeben können, das nur fünf Prozent entspricht, dürfen wir es mit der Geometrie wohl nicht allzu genau nehmen. In diesem Fall kann auch nicht die Länge als Ersatzmaß dienen, da acht Prozent wahlweise gleich lang wie fünf oder dreizehn Prozent erscheint.

Mir geht es jedoch weder darum, Schulbuchverlage anzupatzen, noch darum, diese Schieflage bei der Verteilungsgerechtigkeit schönzureden. Ich will lediglich darauf aufmerksam machen, dass gewisse Design-Entscheidungen mit Vorsicht zu genießen sind. Immerhin entsteht in Abbildungen wie diesen der Eindruck, dass die Ausprägung noch stärker ist, als die Berechnungen ergeben haben.

Nichtsdestotrotz werde ich in meinem Unterricht davon Gebrauch machen, Bananen zur Veranschaulichung zu nutzen. Das Tolle daran ist nämlich, dass man diese Zerlegung natürlich auch mit echten Früchten machen kann. Die Kinder bekommen dafür von mir in Zweierteams jeweils eine solche gepaart mit einem Buttermesser, wodurch sich die Verletzungsgefahr in Grenzen halten sollte, sowie einen Schmierzettel als Unterlage. Ich beispielsweise habe für derartige Zwecke einen Stapel Papier bei meinem Arbeitsplatz liegen, auf den ich u. a. einseitig bedruckte Fehldrucke, nicht benötigte Kopiern, etc. ablege.

Anschließend sollen sie die Banane entsprechend ihrer Vermutung in die sieben Stücke zerschneiden, bevor die Auflösung durch die Lehrperson kommt. Dabei soll die Länge eines Stücks den jeweiligen Anteil der Stakeholder widerspiegeln, d. h. wir ignorieren das oben beschriebene Problem der ungleich geformten Frucht und nutzen stattdessen den Vorteil einer einprägsameren Methode, bei die Lernenden nicht nur zuhören und schreiben, sondern auch selbst etwas tun müssen:

Eine weniger klebrige Alternative wäre, stattdessen mit Centmünzen zu arbeiten. Allerdings müsste die Lehrperson dafür Kleingeld in Klassenstärke bereitstellen, was nicht allzu praktikabel erscheint. In diesem Fall würde ich stattdessen empfehlen einen fiktiven Kaufpreis zu nennen, von dem die Lernenden dann entsprechende Teilbeträge abzwacken und diese aufschreiben (wir ignorieren in diesem Fall den Umstand, dass es um einen Kilopreis und nicht um einen Stückpreis geht - wie z. B. hier).

Die beiden Varianten könnten auch miteinander kombiniert werden. Ich erachte sie als altersadäquat für die fünfte Schulstufe, da es in beiden Fällen kein Problem darstellt, wenn die Kinder noch keine Prozentrechnung kennen. Selbstverständlich müssen jedoch Begriffe wie Import, Export, etc. im Vorhinein erläutert werden, damit klar ist, was zugeordnet werden soll. Vielleicht bleibt danach ja sogar noch Zeit, um zu thematisieren, wie mit fehlerbehafteten Veranschaulichungen getrickst werden kann.

Johannes C. Huber (hat nun auch als Lehrer in der Schule jeden Tag eine Banane als Jause dabei)

Nein, das andere rechts!

Thema: Software und Koordinatensysteme

Obwohl manche Menschen mit räumlicher Geometrie zu kämpfen haben, sind wir grundsätzlich recht gut darin, uns in einer dreidimensionalen Umgebung zurechtzufinden. Sobald unser Vorstellungsvermögen einigermaßen mit dem kartesischen Koordinatensystem vertraut ist, erweitern wir dieses noch um eine weitere Achse und können uns somit in alle erdenklichen Richtungen bewegen.

Dabei spielt die Orientierung der drei Raumachsen jedoch eine entscheidende Rolle. Es gibt nämlich sogenannte rechts- und linkshändige Koordinatensysteme. Auf den ersten Blick mag man vielleicht keinen großen Unterschied zwischen den beiden Varianten erkennen, aber wir können sie uns, wie der Name schon sagt, ganz einfach mit zwei Händen veranschaulichen. Dazu streckt man jeweils den Daumen, Zeige- und Mittelfinger aus und spreizt die drei so auseinander, dass jeweils ein kleines Koordinatensystem entsteht. Der Daumen stellt dabei die x-, der Zeigefinger die y- und der Mittelfinger die z-Achse dar, wobei diese meist rot, grün und blau gefärbt werden:

Merkhilfe für Links- & Rechtssystem (Bildquelle: Johannes C. Huber)

Ein rechtshändiges System ist vor allem in der Wissenschaft und vermutlich deshalb auch im Schulunterricht gebräuchlich. Es ist mathematisch positiv, aber geodätisch negativ, d. h. gegen den Uhrzeigersinn orientiert. In diesem Fall stellen wir uns vor, dass wir ein zweidimensionales Koordinatensystem auf einem Blatt Papier vor uns liegen haben und es mit einer dritten Achse nach oben erweitern, sodass wir es frontal betrachten (Normalsicht).

Rechtssystem auf einem 200 Franken-Schein (Bildquelle: Johannes C. Huber)

Ein linkshändiges System, hingegen, ist mathematisch negativ, aber geodätisch positiv, d. h. im Uhrzeigersinn orientiert. Dazu können wir uns vorstellen, dass wir ein zweidimensionales Koordinatensystem auf einem Bildschirm sehen, welches wir mit einer dritten Achse in das Display hinein erweitern, sodass wir es aus der Vogelperspektive betrachten (Draufsicht). Linkssysteme kommen unter anderem in der Geodäsie und bei Pixelgrafiken zum Einsatz, wobei im letzteren Fall die positive y-Achse nach unten zeigt.

So weit so gut, aber was genau ist jetzt das Besondere an den beiden Systemen? Immerhin können wir in beiden letzendlich die gleichen Dinge tun. Es kommt also eigentlich nur darauf an, welche Orientierung man bevorzugt. Die Eigenschaften mathematisch und geodätisch positiv bzw. negativ beruhen auf dem Drehsinn der Achsen (ähnlich wie bei der Drehrichtung von Gewinden von Schrauben). Um diesen zu ermitteln, schauen wir uns an, in welche Richtung wir den positiv bzw. negativ orientierten Richtungsvektor einer Achse drehen müssten, um auf dem kürzesten Weg zum entsprechenden Richtungsvektor der nächsten zu kommen.

Eine einfache Möglichkeit, um die Orientierung der Achsen rechnerisch festzustellen, ist das Spatprodukt (Skalarprodukt des Kreuzprodukts zweier Vektoren und eines dritten Vektors) ihrer positiven Richtungsvektoren zu bilden. Falls dieses positiv ist, handelt es sich um ein Rechtssystem und falls nicht, handelt es sich um ein Linkssystem.

Der wesentliche Unterschied zwischen einem Links- und einem Rechtssystem ist, dass wir das eine nicht ohne Spiegelungen in das andere überführen können. In anderen Worten: Wir können ein Rechtssystem so lange drehen, wie wir wollen, aber es wird trotzdem niemals ein Linkssystem daraus werden und umgekehrt. Das würde mathematisch gesehen nämlich einer nicht-zyklischen Vertauschung der Einheitsvektoren des entsprechenden Vektorraums entsprechen.

Viele Computerprogramme arbeiten mit Koordinatensystemen. Dabei gibt es anscheinend keinen einheitlichen Standard, aber durchaus eine Tendenz in Richtung Rechtssysteme. Zusätzlich dazu wird noch unterschieden, ob dabei die y- oder z-Achse nach oben zeigt. Ich habe mich informiert, welche Programme mit welcher Variante arbeiten und meine Erkenntnisse in Form einer Übersicht, die an jene von Ahmed Yasin Burul und Freya Holmér angelehnt ist, festgehalten (kein Anspruch auf Vollständigkeit):

 
Orientierung der Koordinatenachsen in verschiedenen Computerprogrammen* (Bildquelle: Johannes C. Huber)

Derartige Software kommt beispielsweise in der Mathematik und den Naturwissenschaften, in der Architektur, beim 3D-Druck oder der 3D-Animation und im Game Design zum Einsatz. Personen, die verschiedene Programme verwenden, müssen sich unter Umständen mit Rechts- und Linkssystemen auseinandersetzen, da es unter anderem zu Darstellungsfehlern kommen kann, falls Dateien in unterschiedlichen Umgebungen bearbeitet werden. Mithilfe von Skripten können jedoch, unabhängig von der Orierntierung der Achsen, Transformationen durchgeführt werden, um die Koordinaten aus einem System in ein anderes zu übertragen und so etwaige Probleme zu vermeiden.

Johannes C. Huber (achtet beim Anwenden der Handregel darauf, nicht nur die z-Achse zu zeigen)

* Hier eine genaue Auflistung der Software in der Übersicht:
Rechtssysteme mit y-Achse oben: Adobe Substance 3D Painter, Autodesk Maya, Autodesk Softimage (früher XSI), Houdini, Minecraft, Modo, OpenGL, Roblox Studio, Verge3D
Rechtsysteme mit z-Achse oben: Archicad, Autodesk 3DS Max (war früher ein Linkssystem), Autodesk AutoCAD, Blender, Cryengine, Gam3d, GeoGebra, SketchUp, Ultimaker CURA, Valve Source²
Linkssysteme mit y-Achse oben: Lightwave 3D, Maxon Cinema 4D, Microsoft Direct3D/X, Unity, ZBrush
Linkssysteme mit z-Achse oben: Unreal Engine

Quellen:

• Rechts- und Linkssystem in Mathe online
• Koordinatentransformationen in Cinema 4D
• Unterschied zwischen Umgebungs- und Objektkoordinaten in Cinema 4D
  
• Koordinatensysteme in OpenGL
• Portieren von einem System in ein anderes in Direct3D
  
• Transformation über Parameter auf IN DUBIO PRO GEO
  
• Tabelle der Orientierungen in verschiedenen Programmen

Der Rubel rollt bergauf

Thema: Geldstrafen und Logarithmen

Dieser Beitrag ist am 05.11.2024 auch im Standard erschienen.

Vor Kurzem wurde im Standard ein Artikel über die Höhe einer Entschädigungsauflage (in anderen Worten: Strafzahlung) berichtet, zu der Google von einem russischen Gericht verurteilt wurde. Dabei geht es um den atemberaubenden Betrag von umgerechnet ungefähr 20 Quintilliarden US-Dollar, welcher die gesamte auf der Welt verfügbare Geldmenge bei Weitem übersteigt.

Die Geldstrafe betrug ursprünglich 100 000 Rubel, was laut Artikel gerundet in etwa 1 025 US-Dollar entspricht.  Mithilfe einer einfachen Schlussrechnung können wir folgern, dass ein Rubel somit 0,01025 US-Dollar wert sein müsste. Dieser Betrag stimmt tatsächlich recht genau mit dem aktuellen Wechselkurs (Stand: 31.10.2024) von 0,01027 US-Dollar überein.

 Das signierte Andenken eines Couchsurfers, der vor ein paar Jahren bei unserem Autor zu Gast war, ist derzeit ungefähr einen US-Dollar wert. (Bildquelle: Johannes C. Huber)

Allerdings gilt der Zusatz, dass diese nach jeder Woche verdoppelt wird, und zwar grundsätzlich unbegrenzt. Doch wie viele Wochen sind seit der Ankündigung der Strafe bereits vergangen, um auf einen dermaßen abgehobenen Betrag zu kommen? Um das auszurechnen, basteln wir uns nun eine passende Formel. Um den Geldbetrag in US-Dollar einmal zu verdoppeln, multiplizieren wir ihn mit der Zahl zwei. Nach einer Woche, hat sich die Strafe also beispielsweise bereits auf 1 025 · 2 = 2 050 verdoppelt. Nach zwei Wochen auf 1 025 · 2 · 2 = 2 050 · 2 = 4 100 und so weiter.

Diese Überlegung können wir für jede weitere Woche fortsetzen, aber anstatt eine immer länger werdende Kette von Multiplikationen mit Zweiern aufzuschreiben, nutzen wir die Potenzschreibweise. Da wir es mit einer kontinuierlichen Verdopplung zu tun haben, wählen wir als Basis die Zahl zwei und als Exponent schreiben wir einen Platzhalter n für die gewünschte Anzahl der Wochen: 1 025 · 2ⁿ. Falls wir beispielsweise wissen möchten, wie hoch die Strafe nach acht Wochen ist, ersetzen wir einfach die Variable n mit der Zahl acht und sehen, dass sich die Strafe bereits auf 1 025 · 2⁸ = 1 025 · 256 = 262 400 erhöht hat.

Als Nächstes stellen wir eine Gleichung auf, die den aktuellen Sachverhalt darstellt. Wir wissen, dass die Höhe der Strafe mittlerweile etwa 20 Quintilliarden US-Dollar beträgt, also gilt:

1 025 · 2ⁿ = 20 000 000 000 000 000 000 000 000 000 000 000

Wenn wir diese nach n auflösen, erhalten wir die Anzahl der Wochen, die vergangen sein müssten, um auf den aktuellen Betrag der Geldstrafe zu kommen. Dazu dividieren wir zunächst beide Seiten durch 1 025:

2ⁿ = 19 512 195 121 951 200 000 000 000 000 000

Im nächsten Schritt arbeiten wir mit Logarithmen. Aufgrund der Rechengesetze für Potenzen gilt:

ln(2) · n = ln(19 512 195 121 951 200 000 000 000 000 000)

Um nun die Zahl n auszurechnen, müssen wir lediglich beide Seiten durch den natürlichen Logarithmus der Zahl zwei dividieren. Ein handelsüblicher Taschenrechner wird damit aber aufgrund der schieren Größe der ursprünglichen Zahl auf der rechten Seite der Gleichung Probleme haben, weshalb wir uns mit Online-Tools wie beispielsweise Wolfram Alpha Abhilfe verschaffen können. Wir kommen so auf eine Näherungslösung von ungefähr 104 Wochen bzw. zwei Jahren**.

Johannes C. Huber (еще нужно попрактиковаться в кириллице)

* Wir könnten das Gleiche auch mit Rubel machen und würden so in weiterer Folge bei 100 000 · 2ⁿ = 1 951 219 512 195 120 000 000 000 000 000 000 000 landen. Das Resultat für n ändert sich dadurch jedenfalls nicht.

** Die neunmonatige Frist für die Erfüllung der Auflagen wurde hier nicht mit eingerechnet.

Wann läutet es, Herr Professor?

Thema: Wanduhren und Schulmathematik

Mit Beginn dieses Schuljahres habe ich den nächsten Schritt auf der schulischen Karrierleiter gewagt und darf nun als Klassenvorstand eine erste Klasse begleiten. Zu den vielen Aufgaben, die nicht dezidiert in meiner Jobbeschreibung stehen, zähle ich auch das Einrichten des Klassenraums. Da wir keine Uhr hatten, habe ich das als Anlass genommen, endlich eine von den unzähligen "mathematischen" zu besorgen:

Klassenuhr Version 1.0 (Bildquelle: Johannes C. Huber)

Dekoelemente wie diese wecken im Idealfall gleich unsere Neugier à la "Ich weiß, dass an dieser Stelle jene Zahl stehen muss, aber warum?". Es gibt unzählige solche Ziffernblätter mit unterschiedlicher Komplexität im Internet zu finden. Ich habe mich für diese Variante entschieden, weil sie eine ausgewogene Mischung an Teilbereichen abdeckt und außerdem, meiner Meinung nach, einen gutes Mittelmaß zwischen einfacher und höherer Mathematik darstellt.

Ziffernblatt der Uhr (Bildquelle: Johannes C. Huber)

Die meisten Einträge auf der Uhr lassen sich mit Mathematik aus dem Schulstoff beantworten. Allerdings gehen manche davon ein wenig über die üblichen Themenbereiche hinaus:

• 1 (11. Schulstufe): Dazu müssen wir die sogenannte Eulersche Identität kennen:
  

  
  

  Aus der Gleichung ergibt sich, dass die Eulersche Zahl e hoch die Kreizahl Pi mal die imaginäre Einheit i die Zahl -1 ergibt. Die Gegenzahl dieses Ausdrucks ist somit 1.
  
• 2 (10. Schulstufe): Hier haben wir es mit einer unendlichen geometrischen Reihe zu tun. Das Sigma steht für eine Summe. Rechts davon steht der Term, der uns sagt, wie die Glieder der Reihe bzw. die Summanden beschaffen sind. Diese werden laufend zusammengezählt. Die Laufvariable i unter dem Sigma legt den Startpunkt (hier die Zahl 0) fest und die Lemniskate darüber bedeutet, dass wir diesen Prozess, zumindest theoretisch, unendlich lange fortsetzen. Das erste Glied der Reihe ergibt ein Ganzes, das zweite ein Halbes, das dritte ein Viertel, das vierte ein Achtel und so weiter. Die Zwischensumme wächst zwar immer weiter an, aber auch mit jedem Summand nur mehr halb so viel wie davor. Die ersten paar Zwischensummen lauten 1 - 1,5 - 1,75 - 1,875 - ... Der Grenzwert der Reihe, gegen die sie strebt, ist 2. Diesen Umstand können wir uns auch schön veranschaulichen:
  

  

• 3 (10. Schulstufe): Der natürliche Logarithmus zur Basis e (ln - logarithmus naturalis) der Zahl 21 ist 3,0445224377234229965005979803657... und kaufmännisch abgerundet ungefähr 3.
• 4 (10. Schulstufe): Der Logarithmus zur Basis 10 (lg - logarithmus generalis bzw. dekadischer Logarithmus) der Zahl 10 000, die hier vermutlich aus Platzgründen als Hochzahl geschrieben steht, ist die Zahl 4. Da es sich bei 10 000 um eine Potenz von 10 handelt, können wir stattdessen auch einfach die Anzahl der Nullen zählen.
  
• 5 (7. Schulstufe): Hier sehen wir das kleinste nichttriviale* pythagoräische Tripel als rechtwinkliges Dreieck mit den beiden Kathetenlängen 3 und 4 veranschaulicht. Dabei handelt es sich um drei ganze Zahlen a, b und c, die zusammen den pythagoräischen Lehrsatz a² + b² = c² erfüllen. Die fehlende Zahl bzw. die Länge der Hypotenuse im Dreieck ist 5, da 3² + 4² = 5².
  
• 6 (11. Schulstufe): Diese Notation steht für eine dreielementige Menge A. Wir sollen die Anzahl der Permutationen, d. h. die Anzahl der verschiedenen Möglichkeiten, um ihre (voneinander unterscheidbaren) Elemente anzuordnen, bestimmen. Das ist in diesem Fall auf 3! = 3 ⋅ 2 ⋅ 1 = 6 verschiedene Arten möglich, da es drei Auswahlmöglichkeiten für das erste Elemente gibt, zwei für das zweite und nur eine für das noch verbleibende. Zur Veranschaulichung: Angenommen die drei Elemente heißen x, y und z, dann lauten die Permutationen xyz, xzy, yxz, yzx, zxy und zyx.
  
• 7 (6. Schulstufe): Hierzu muss man wissen, dass ein Siebtel auch als die Dezimalzahl 0,142857... dargestellt werden kann. Der Kehrwert dieser Zahl ist also 7.
  
• 8 (7. Schulstufe): Die Kubikzahl bzw. dritte Potenz von 2 ist 8.
• 9 (5. Schulstufe): Hierbei dürfte es sich um ein sogenanntes magisches Quadrat handeln, in das wir die Zahlen von 1 bis 9 einsetzen müssen, um in jeder Zeile und Spalte die Summe 15 zu erhalten. Damit das auch entlang der Diagonalen funktioniert, müsste die Zahl 5 im Zentrum stehen. Allerdings wissen wir hier bereits, dass dort die 9 stehen muss. In diesem Fall gilt die Summe also nur für die Zeilen und Spalten. Das vollständig ausgefüllte magische Quadrat sieht dann so aus:
  

  

• 10 (6. Schulstufe): 9,999... ist eine andere Darstellung der Zahl 10. Eine Möglichkeit, um diesen Umstand plausibel zu machen, ist die Bruchdarstellung. 0,111... ist ein Neuntel als Dezimalzahl, also muss das Neunfache davon, nämlich 0,999... gleich neun Neuntel bzw. ein Ganzes sein. Somit ist in diesem Fall auch 9 + 0,999... = 9 + 1 = 10.
  
• 11 (7. Schulstufe): Die Quadratwurzel von 121 ist 11**.
  
• 12 (9. Schulstufe): Hierbei handelt es sich um die Zahl 12 in der Zahlendarstellung zur Basis 2 (Binärsystem), da 1 ⋅ 2³ + 1 ⋅ 2² + 0 ⋅ 2¹ + 0 ⋅ 2⁰ = 12.
  

Meine Erstklässler haben mich übrigens gleich damit konfrontiert, dass sie diese Uhr nicht lesen können. Das liegt allerdings nicht an der Beschriftung, sondern ganz einfach daran, dass sie sich noch schwer damit tun, analoge Uhren zu lesen. Ich habe nicht klein bei gegeben, weil es mir wichtig ist, dass sie auch diese Kulturtechnik beherrschen. Als Kompromiss, der hoffentlich auch zur allgemeinen Pünktlichkeit beiträgt, habe ich dann aber die alte Uhr aus meiner Wohngemeinschaft aufgehängt:

Klassenuhr 2.0 (Bildquelle: Johannes C. Huber)

Auf dem Ziffernblatt habe ich den Kindern außerdem die Pausenzeiten in verschiedenen Farben aufgemalt, damit sie besser einschätzen können, wie viel Zeit sie noch haben. Sobald der Minutenzeiger den entsprechenden Kreisringsektor überquert hat, ist die jeweilige Pause vorbei. Bis jetzt funktioniert unser System vergleichsweise gut. Mit etwas Übung dürfte auch das Lesen der analogen Uhr kein Problem mehr darstellen und ich kann wieder eine mathematischere Variante aufhängen.

Herzlichen Dank für wertvollen Input von Sergey und Christina!

Johannes C. Huber (möchte irgendwann auch selbst ein mathematisches Ziffernblatt gestalten)

* Das kleinste triviale Tripel ist 0² + 0² = 0². Andere wären z. B. 1² + 0² = 1² und so weiter.

** An dieser Stelle möchte ich auf eine Fehlvorstellung in Zusammenhang mit dem Wurzelziehen hinweisen. Manchmal wird nämlich behauptet, dass jede reelle Zahl (außer 0) zwei Quadratwurzeln hat. Das hängt damit zusammen, dass wir diesen Sachverhalt als quadratische Gleichung angeben können. In diesem Fall ist neben 11 auch -11 eine Lösung der Gleichung x² = 121, da das negative Vorzeichen durch das Quadrieren verschwindet. So weit so richtig, doch die Quadratwurzel einer Zahl ist eindeutig als nicht negativ definiert. In anderen Worten: Auf die Frage, welche reelle Zahl quadriert werden muss, um eine bestimmte zu erhalten, gibt es (außer bei 0) zwei Antworten, aber auf die Frage, was die Quadratwurzel einer reellen Zahl ist, gibt es nur eine.

Stellenwertschreibweise mit dem Pumuckl

Thema: Kobolde und Stellenwerte

Als kurze Wiederholung der Stellenwertschreibweise von Dezimalzahlen, frage ich meine erste Klassen gerne, ob sie schon zu jung für den Pumuckl sind oder die Figur noch kennen. Anscheinend gab es über die Jahre ausreichend Serien- und Filmmaterial, sodass die meisten zumindest schon einmal von dem frechen Kobold gehört haben, der das Leben vom Schreinermeister Eder auf den Kopf stellt.

Man sollte nicht einfach mit Ziffern um sich werfen. (Bildquelle: Johannes C. Huber)

Nachdem geklärt ist, was der Pumuckl so treibt, konfrontiere ich sie mit dieser Aufgabe:

Der Pumuckl hat die Stellenwerte einer Zahl von klein nach groß sortiert.
Leider hat er die Reihenfolge falsch verstanden.

1ZT   2M   3Z   4ZM   5E   6HT   7T   8HM   9H

1. Was ist hier schiefgelaufen? Erkläre den Denkfehler!
2. Wie heißt die Zahl? Schreib sie auf!

Meister Eder hat ihm dann erklärt, dass die richtige Reihenfolge mit den Buchstaben zu tun hat.
Also hat er es noch einmal versucht.

9E   2H   1HM   9HT   5Md   6T   9Z   7ZM   8ZT

1. Was ist hier schiefgelaufen? Erkläre den Denkfehler!
2. Wie heißt die Zahl? Schreib sie auf!

Bei der ersten Aufgabe schauen wir vorrangig darauf, dass die Kinder die richtige Reihenfolge der Stellenwerte im Kopf haben und die Zahl anschließend in Dreierpaketen (Einer, Tausender, Millionen, etc.) aufschreiben, damit sie gut lesbar ist. Bei der zweiten Aufgabe achten wir auch darauf, ob sie berücksichtigen, dass keine Millionen angegeben sind und bei diesem Stellenwert eine Null aufschreiben.

Johannes C. Huber (hat die Stimme vom Pumuckl immer als furchtbar nervig empfunden)

Lösungen:
Beim ersten Mal hat er stattdessen die Ziffern der Stellenwerte von klein nach groß bzw. in aufsteigender Reihenfolge geordnet.
Richtig sortiert wäre es 8 HM   4ZM   2M   6HT   1ZT   7T   9H   3Z   5E und als Zahl: 842 617 935.

Beim zweiten Mal hat er stattdessen die Kürzel der Stellenwerte von A bis Z bzw. in alphabetischer Reihenfolge geordnet.

Richtig sortiert wäre es 5Md   1HM   7ZM  9HT   8ZT   6T   2H   9Z   9E und als Zahl: 5 170 986 299.

Einfach bei 0,625 anläuten

Thema: Türschilder und Bruchrechnung

Bei einer Fortbildung für das Unterrichtsfach Mathematik wurde uns ein Online-Rechner vorgestellt, mit dem man Aufgaben lösen kann, die auf Bildern zu sehen sind. Wie wir spätestens seit ChatGPT wissen, ist jedoch nicht alles Gold, was glänzt. Also habe ich mir den Spaß gemacht und ausprobiert, was das Programm alles als Rechnung interpretiert und bin auf ein paar nette Funde gestoßen.

In diesem Beitrag geht es um das Thema Bruchrechnung im Allgemeinen und Doppelbrüche im Speziellen. Ich habe nämlich unter anderem das Bild eines Türplans aus dem Eingangsbereich in einem Wohnhaus hochgeladen, um zu überprüfen, ob das Programm die Angaben als Doppelbrüche interpretiert und ausrechnet. Das Ganze hat dann auch wie erwartet funktioniert:

Der Mathe-Löser in Microsoft Edge im Einsatz. (Bildquelle: Johannes C. Huber)

Ich habe mir den Spaß gemacht, eine entsprechende Installation vorzunehmen:

Der freundliche Mathematiker aus der Nachbarschaft hat wieder zugeschlagen. (Bildquelle: Johannes C. Huber)

Johannes C. Huber (hofft, dass die Hausgemeinschaft es als Kunst und nicht als Vandalismus sieht)

Ein statistisches Problem von Ziffernnoten

Thema: Leistungsbeurteilungen und Skalenniveaus

Im Schulsystem sind wir hin und wieder gezwungen, Statistik für die Protokollierung von verschiedenen Dingen zu zweckentfremden. Ein solcher Fall tritt beispielsweise bei Notenstatistiken von Schularbeiten auf. Wenn dafür lediglich eine Liste o. ä. angelegt werden müsste, wäre das kein Problem, aber leider müssen wir dabei mitunter auch Durchschnittsnoten für die ganze Klasse berechnen.

Dieser Zahlenwert ist allerdings streng genommen Schwachsinn, weil seine Bildung nicht ganz einwandfrei ist. In der Statistik arbeiten wir mit Daten, d. h. wir untersuchen verschiedene Werte und bilden auch viele Kennzahlen, die sich mit ihnen ermitteln lassen. Dabei unterscheiden wir zwischen sogenannten Skalenniveaus und meinen damit unterschiedliche Güteklassen von Daten:

Nominalskala

Die einfachste Form sind nominal skalierte Daten, die einfach nur eine bestimmte Eigenschaft beschreiben. Das können beispielsweise Farben (Haar-, Augen-, Lieblingsfarbe, etc.), Orte (Wohn-, Urlaubs-, Geburtsort, etc.), Namen, Muttersprachen, Staatsbürgerschaften, Postleitzahlen, Kennzeichen, Automarken und so weiter sein. Mit dieser Art von Daten können wir Vergleiche anstellen, d. h. entscheiden, ob zwei Werte gleich sind oder eben nicht. Abgesehen davon können wir sie lediglich zählen und dabei feststellen, ob es einen Wert gibt, der am häufigsten auftritt (der Modus oder Modalwert).

Ordinalskala

Das nächste Skalenniveau sind ordinal skalierte Daten. Werte dieser Art können wir nicht nur sortieren, sondern auch ordnen. Dadurch lässt sich auch der Wert in der Mitte (der Median) bestimmen. Typische Beispiele für Ordinalskalen sind u. a. die Leuchtkraft von hell bis dunkel oder Konfektionsgrößen für Kleidung. Insbesondere logarithmische Skalen wie z. B. ph-Werte, Lautstärke in Dezibel, der Visus (die bei einem Sehtest gemessene Sehstärke), die Intensität von Erdbeben auf der Richter-Skala oder von Vulkanausbrüchen mittels Vulkanexplosivitätsindex fallen ebenfalls in diese Kategorie.

Darüber hinaus gibt es auch viele Beispiele, bei denen eine Skala zum Einsatz kommt, die zwar das Bilden einer Rangliste ermöglicht, aber bei genauerer Betrachtung keine einheitliche Regel für den Abstand zwischen den Werten aufweist. Dazu zählen beispielsweise die Windstärke auf der Beaufort-Skala, der Härtegrad von Mineralen auf der Mohs-Skala oder der Schärfegrad von Paprikas auf der (ursprünglich subjektiv gemessenen) Scoville-Skala. Generell fallen viele Dinge, die man subjektiv bewerten kann hier hinein. Bei Umfragen kommt häufig eine sogenannte Likert-Skala zum Einsatz, um Zustimmung oder Abneigung zu einer bestimmten Aussage auszuwählen.

Ein weiteres Beispiel, dass ich meinen Lernenden gerne nenne, sind Levelsysteme in Videospielen wie Pokémon oder Brawl Stars, weil den meisten Kindern dann gleich klar ist, dass man normalerweise nach jedem Aufstieg zumindest ein bisschen mehr machen muss als bisher, um in ein noch höheres Level aufzusteigen. Das ist auch der wesentliche Unterschied zum nächsthöheren Skalenniveau, denn um mit den Werten rechnen zu können, müssen die Abstände zwischen den Einheiten auf der Skala auch wirklich einheitlich sein. 

Kardinalskala

Die kardinal skalierten Daten beinhalten zwei Skalenniveaus. Mit Daten auf einer Intervallskala können wir immerhin schon addieren und subtrahieren, weil die Abstände zwischen den Einheiten auf der Skala überall gleich groß sind. Dazu zählen beispielsweise viele Zeitangaben, wie Geburts-, Sterbe-, Ernte-, Ablauf- oder Mindeshaltbarkeitdaten. Abgesehen davon fallen auch der Intelligenzquotient und Temperaturskalen wie Grad Celsius oder Grad Fahrenheit in diese Kategorie. Ab hier kann außerdem der arithmetische Mittelwert berechnet werden.

Die höchste Güteklasse sind metrisch skalierte Daten. Man sagt dazu auch Ratio- oder Verhältnisskala. Das Besondere daran ist, dass diese zusätzlich zur Eigenschaft einheitlicher Abstände auch noch einen natürlichen Nullpunkt haben, weshalb wir sie auch mit Zahlen multiplizieren und durcheinander dividieren können. Dadurch kann auch das geometrische Mittel berechnet werden. Ein paar einfache Beispiele dafür sind Alter, Geldpreis, Geschwindigkeit, Masse, Länge, Fläche und Volumen. Bei den Temperaturskalen qualifiziert sich jene mit der Einheit Kelvin für dieses Skalenniveau, weil diese einen absoluten Nullpunkt hat.

Nun sollte das Problem mit der Notenstatistik klar sein. Die Ziffernnoten in der Schule sind jedenfalls nicht metrisch skaliert, weil die Abstände zwischen den aufeinanderfolgenden Noten nicht einheitlich groß sind. Ich habe hier ein paar Beispiele von verschiedenen österreichischen Schulen angeführt:

Beurteilungsschlüssel für Schularbeiten des BG/BRG Weiz (Bildquelle: BG/BRG Weiz)

Beurteilungsschlüssel für Schularbeiten des BG/BRG/BORG Eisenstadt (Bildquelle: BG/BRG/BORG Eisenstadt)

 
 Beurteilungsschlüssel für Schularbeiten der MS Rankweil OST (Bildquelle: MS ROST)

Es ist also eigentlich schlichtweg falsch, hier einen Durchschnitt zu berechnen. Eine Möglichkeit, diese Umstand zu umgehen, wäre stattdessen z. B. erst die durchschnittliche Anzahl an Punkten bei einer Schularbeit oder einem Test zu berechnen und im Anschluss daraus eine Durchschnittsnote abzuleiten. Das hat allerdings zu Folge, dass dieser Wert stets ganzzahlig ist.

Die seit ein paar Jahren zusätlich dazu geltende Unterscheidung zwischen Standard und Standard AHS-Noten habe ich hier der Einfachheit halber einmal weggelassen. Man munkelt auch, dass die gleichen Beurteilungen in unterschiedlichen Unterrichtsfächern oder bei unterschiedlichen Lehrkräften nicht gleich viel Aufwand bedeuten, aber dieses Fass ohne Boden möchte ich an dieser Stelle nicht öffnen.

Mir ist es bereits in meiner Studienzeit befremdlich erschienen, dass ich bei der Einreichung meiner Unterlagen für den Bachelorabschluss eine Durchschnittsnote ausrechnen und (händisch!) auf einem Formular eintragen musste. Womöglich wollte das Studienservicecenter nur noch ein letztes Mal sicherstellen, ob der angehende Mathematiklehrer auch einen Mittelwert korrekt bestimmen kann. Vielleicht sollte aber auch nur getestet werden, ob ich einen Aufschrei aufgrund des völlig unpassenden Skalenniveaus machen würde. Im letzteren Fall habe ich diesen Test wohl nicht bestanden, aber das hat meinen Studienabschluss zum Glück nicht verhindert.

Johannes C. Huber (ärgert sich nicht aufgrund der Noten beim Ausfüllen der Schularbeitsstatistik)

Echte Symbole mit falschen Bedeutungen Teil 1

Thema: mathematische Notation und ihre Herkunft

Im Rahmen dieser Beitragsreihe beschäftige ich mich mit verschiedenen Fehlvorstellungen zu mathematischer Notation. Diesmal geht es um drei allgemein bekannte Symbole:

Wer schon einmal einen Taschenrechner in der Hand gehabt hat, kennt wahrscheinlich dieses Zeichen für die Division: ÷. Es wird Obelus (lat. Bratspieß) genannt und ist im Gegensatz zu / und : kein Bestandteil einer Computertastatur ohne Ziffernblock. Da ein Bruch im Grunde nichts anderes als eine Division ist, liegt die Vermutung nahe, dass es sich bei der Linie in der Mitte um einen Bruchstrich handelt und die beiden Punkte als Platzhalter für Zähler und Nenner agieren. Dafür gibt es jedoch keinerlei Belege. Hinzu kommt, dass dieses Symbol früher unter anderem auch für andere Operationen wie beispielsweise die Subtraktion verwendet wurde, weshalb es nicht eindeutig der Division zugeordnet werden kann.

Das Wurzelsymbol √ erinnert an den klein geschriebenen Buchstaben r. Aus diesem Grund wird oft die Verbindung zum Wort Radix (lat. Wurzel) gezogen. Die Wurzel einer Zahl kann jedoch nicht nur auf diese Art dargestellt werden. Im Schulunterricht kommt unter anderem auch die Schreibweise mit einem Bruch als Exponenten vor. Früher wurden Wurzeln tatsächlich zeitweise mit einem R gekennzeichnet. Es konnte allerdings bis heute nicht zweifelsfrei nachgewiesen werden, worauf das Schriftzeichen tatsächlich basiert.

Das Zeichen für die Unendlichkeit ∞ lässt sich mathematisch als sogenannte Lemniskate (eine besondere in sich geschlossene Kurve) oder  umgangsssprachlich auch als umgefallener Achter beschreiben. Ein weit verbreiteter Irrglaube in Zusammenhang mit dem Ursprung dieses Zeichens, ist, dass es einen sogenannten Ourobouros darstellen soll. Das liegt daran, dass es an eine Schlange, die sich selbst in den Schwanz beißt, erinnert. In Wirklichkeit kann jedoch nicht mit Sicherheit gesagt werden, warum genau dieses Zeichen für die Unendlichkeit gewählt wurde. Nichtsdestotrotz haben derlei modernere Interpretationen fast schon etwas Poetisches.

Johannes C. Huber (muss zugeben, dass er all diesen Geschichten zunächst selbst auf den Leim gegangen ist)

Eine Frage des Spielraums

Thema: Fußballfelder und Flächenmaße

Dieser Beitrag ist am 15.04.2024 auch im Standard erschienen. 

Ich habe vor Kurzem das Buch Endspiel des Schweizer Biologen Claude Martin gelesen. Im zweiten Kapitel schreibt er über die sogenannte Walddegradation oder in anderen Worten den Verlust von Wald. Abgesehen von gezielter Rodung, um Waldflächen in Acker- oder Bauland zu verwandeln, können auch Holzeinschlag, Brände und Schädlings- oder Krankheitsbefall dazu führen, dass Wälder verschwinden. Dieser Rückgang von Waldgebieten wird normalerweise in Quadratkilometern pro Jahr angegeben.

Umgangssprachlich ist in diesem Zusammenhang häufig die Rede von Fußballfeldern pro Minute, um Leuten die Möglichkeit zu geben, sich das Ganze besser vorzustellen. Diese recht plakative Einheit wird deshalb unter anderem auch gerne zur Veranschaulichung von Bodenversiegelung verwendet. Allerdings kritisiert der Autor, dass die Maße eines Fußballfeldes nicht eindeutig festgelegt sind und die damit behaftete Ungenauigkeit. Diesen Standpunkt vertritt auch die Statistikerin Katharina Schüller.

Das hängt damit zusammen, dass es zwar Ober- und Untergrenzen für die Seitenlängen gibt, doch innerhalb dieses Rahmens können die Maße stark variieren. Ich habe mir deshalb die Frage stellt, wie groß diese Unterschiede wirklich sind, welche Auswirkungen das auf Berichte in den Medien haben kann und ob die Fußballfelder pro Minute nicht trotzdem ihre Berechtigung haben.

Zuallererst müssen wir klären, wie groß ein Fußballfeld sein kann. Die Standardgröße für internationale Spiele, auf die sich FIFA und UEFA geeinigt haben, setzt sich aus 105 Metern Länge (Seitenlinie) und 68 Metern Breite (Torlinie) zusammen, womit wir auf insgesamt 105 ⋅ 68 = 7 140 Quadratmeter bzw. ungefähr 0,7 Hektar Fläche kommen:

Standardfeldgröße für internationale Spiele (Bildquelle: Johannes C. Huber)

Das entspricht ungefähr dem Mittelmaß der beiden Parameter, aber zumindest theoretisch wäre auch jede erdenkliche Feldgröße zwischen dem Mindestmaß von 90 ⋅ 45 = 4 050 Quadratmetern...:

theoretische minimale Feldgröße (Bildquelle: Johannes C. Huber)

...und dem Höchstmaß von 120 ⋅ 90 = 10 800 Quadratmetern möglich*:

theoretische maximale Feldgröße (Bildquelle: Johannes C. Huber)

Die maximale Feldgröße deckt also immerhin mehr als doppelt so viel Fläche ab wie die minimale. Der Vorwurf mangelnder Genauigkeit erscheint zunächst durchaus berechtigt zu sein, denn je nachdem wie lang die Maße für die beiden Seitenlängen gewählt werden, kommen wir mit wesentlich mehr oder weniger Feldern aus, um eine bestimmte Waldfläche zu beschreiben.

Als nächstes versuchen wir herauszufinden, ob es in unterschiedlichen Medienberichten Abweichungen gibt und wie stark diese sein können. Dazu müssen wir ermitteln, mit welchen Feldgrößen gerechnet wurde, denn falls es uns gelingt, diese zu bestimmen, können wir auch Vergleiche anstellen. Es gibt mehrere Möglichkeiten, um von der Walddegradation auf die Fußballfelder zu kommen, aber wir werden dafür einfach Quadratkilometer in Quadratmeter und Jahre in Minuten umrechnen. Darum machen wir einen kleinen Exkurs zur Umwandlung von Flächeneinheiten bzw. -maßen.

Um zu verstehen, wie wir von einem Flächenmaß auf das andere kommen, beginnen wir mit den Längenmaßen, da diese deren Ausgangsbasis darstellen. Neben der grundlegenden Längeneinheit Meter lernen wir normalerweise auch, was Milli-, Zenti-, Dezi- und Kilometer sind. Zwischen Metern und Kilometern gibt es außerdem noch Deka- und Hektometer, die in der Schule normalerweise nicht extra behandelt werden, weil sie im Alltag nicht gebräuchlich sind, aber der Vollständigkeit halber nehmen wir sie dazu. Wichtig für uns ist, dass jedes Längenmaß hier zehnmal so groß ist, wie das Vorhergehende. Um von einer Einheit auf die nächstkleinere zu kommen, multiplizieren wir sie also mit der Zahl 10:

Flächen sind allerdings nicht ein-, sondern zweidimensional. Der Zusatz "Quadrat-" im Wort Quadratmeter kommt daher, dass die Flächeneinheit einem Quadrat mit einem Meter Seitenlänge entspricht. In einen Quadratmeter passen deshalb nicht etwa zehn, sondern bereits zehn mal zehn, also hundert Quadratdezimeter hinein. Um bei den Flächenmaßen von einer Einheit auf die nächstkleinere zu kommen, müssen wir also stattdessen mit 10² = 10 ⋅ 10 = 100 multiplizieren:

Ein Quadratkilometer entspricht also einer Million Quadratmeter und ein Jahr ungefähr 60 ⋅ 24 ⋅ 365,25 = 525 960 Minuten. Falls die Walddegradation in Quadratkilometern angegeben ist, wandeln wir diese zuerst in Quadratmeter um. Im nächsten Schritt teilen wir sie durch die Minuten in einem Jahr, um die Quadratmeter pro Minute zu erhalten. Zum Schluss teilen wir diesen Wert noch durch die jeweilige Feldgröße und kommen so auf die Anzahl der Felder.

Falls beispielsweise 120 000 Quadratkilometer Wald pro Jahr gerodet werden, entspricht das ungefähr 32 standardmäßigen Fußballfeldern pro Minute. Falls wir jedoch stattdessen die Mindest- und Höchstmaße für die Seitenlängen heranziehen, kommen wir sogar auf circa 56 Felder bzw. nur auf circa 21 Felder.

Jetzt haben wir alles beisammen, um verschiedene Medienberichte zu analysieren. Um die verwendeten Feldgrößen zu bestimmen, drehen wir den letzten Schritt einfach um und teilen die Quadratmeter pro Minute durch die angegebene Anzahl der Felder. Hier ist zum Beispiel für das Jahr 2017 von 20 Feldern die Rede, da insgesamt circa 76 000 km² Wald gerodet wurden. Allem Anschein nach wurde hier die standardmäßige Feldgröße verwendet, wie wir selbst nachrechnen können:

(76 000 000 000 m² : 525 960 min) : 20 Felder ≈ 7224 m² pro Feld

Die so errechnete Feldgröße ist zwar eigentlich ein bisschen mehr als der Standard, aber das dürfte daran liegen, dass die Anzahl der Felder auf eine ganze Zahl, also in diesem Fall zwanzig, gerundet wurde. Hier und hier sind es für das Jahr 2018 mit 12 000 000 ha und hier für 2022 mit 112 800 km² jeweils 30 Felder. Hier wurde die Abholzung für das Jahr 2021 auf 11,1 Mio. ha beziffert und für das Jahr 2022 mit 11 Feldern angegeben, da diese 4,1 Mio. ha entsprach, was auch hier, hier und hier mit 11 Feldern angegeben wurde. In all diesen Beispielen entspricht der Wert umgerechnet jedenfalls der Standardgröße.

Das ändert sich auch nicht bei Meldungen, die eine bestimmte Region der Erde betreffen. Beispielsweise wurden im Jahr 2011 in Brasilien insgesamt ungefähr 13 000 000 Hektar Wald gerodet, weshalb hier drei Felder pro Minute erwähnt werden. Hier, hier, hier und hier wird das Gleiche für den Zeitraum von Juli 2019 bis August 2020 (11 000 km²) gemacht. Hier werden bei der Abholzung im Amazonasgebiet ebenfalls drei Felder erwähnt. Beim Thema Bodenversiegelung ist es übrigens genauso: Hier dienen dreißig Felder, hier und hier jeweils sechzehn und hier acht als Vergleich.

Obwohl es theoretisch zu Ungenauigkeiten aufgrund variabler Felddimensionen kommen könnte, scheint es so, als ob in der Regel ohnehin stets die Standargröße für Berechnungen herangezogen wird. Dadurch verliert der Vorwurf, zumindest in der Praxis, an Wirkung und es handelt sich, meines Erachtens, trotzdem um eine hilfreiche Einheit, um sich ein besseres Bild davon zu machen. Selbstverständlich gibt es einen klaren Unterschied zwischen den Zahlen und der bildhaften Vorstellung, aber für mich persönlich spielt es keine große Rolle, ob es jetzt statt dreißig doch nur zwanzig oder sogar fünfzig Fußballfelder Waldfläche pro Minute sind, die verschwinden, denn ich finde die Vorstellung in jedem Fall beunruhigend.

Johannes C. Huber (fände es schön, wenn Fußballfelder auch quadratisch sein dürften)

* In der Praxis muss das Feld allerdings rechteckig sein, d. h. ein 90 mal 90 Meter-Quadrat wäre nicht erlaubt und wahrscheinlich auch nicht förderlich für das Spielgeschehen. Wer sich mit den theoretischen Felddimensionen spielen möchte, kann das mit diesem GeoGebra-Applet tun.

Quellen:

• Martin C. (2015): Endspiel. Wie wir das Schicksal der tropischen Regenwälder noch wenden können. S. 37 und 55.
• Schüller K. (2015): Statistik und Intuition. Alltagsbeispiele kritisch hinterfragt. S. 21.
• UEFA (2011): UEFA-Handbuch für Qualitätsstadien.
• UEFA (2018): UEFA-Stadioninfrastruktur-Reglement.

Rätselhafte Namen Teil 1

Thema: Buchstaben und Stellenwerte

Für meinen 50. Blogbeitrag wollte ich etwas Besonderes machen. Ein Gedanke, der schon länger in meinem Kopf herumgegeistert ist, war, ein eigenes Rätsel zu erstellen. Im Zuge meiner Ideenfindung bin ich durch Zufall auf den Namen Simon Phillips Norton gestoßen. Dabei handelt es sich um einen recht obskuren Mathematiker aus Großbritannien. Wenn man Alexander Masters, der seine Biographie verfasst hat und zeitweise auch sein Untermieter war, glauben darf, hat er Leuten, die sich auf sein Wohnungsinserat gemeldet hatten, manchmal folgendes Rätsel gestellt: SIMON ⋅ P = NORTON.

Das Ziel ist herauszufinden, mit welchen Ziffern die Buchstaben ausgetauscht werden müssen, damit die Rechnung aufgeht. Anscheinend gibt es in diesem Fall sogar zwei mögliche Lösungen. In diesem Beitrag werde ich zeigen, wie ich selbst auf eine davon gekommen bin.

Zu Beginn ist es ratsam, sich den Aufbau des Rätsels genauer anzsehen. Hinter den Buchstaben steckt eine fünfstellige Zahl, die mit einer einstelligen multipliziert wird. Das Ergebnis ist eine sechsstellige Zahl:

ZT T  H  Z  E  ⋅  E  =  HT ZT T  H  Z  E
S I M O N ⋅ P = N O R T O N

Dabei fällt uns auf, dass manche Buchstaben mehr als einmal vorkommen: Sowohl O, als auch N sind beide gleich dreimal vertreten. Insgesamt sind es acht verschiedene Buchstaben, weshalb wir auch nach bis zu acht verschiedenen Ziffern suchen müssen.

Zunächst einmal konzentrieren wir uns auf die Einer- und Zehnerstellen, da dort die beiden Buchstaben O und N in derselben Reihenfolge vorkommen. Wir suchen also nach zwei Ziffern, die mit P multipliziert beim Ergebnis gleich bleiben.

Um mir einen Überblick zu verschaffen, habe ich alle möglichen Multiplikationen von N mit P in einer Tabelle aufgelistet. Da es zehn verschiedene Ziffern gibt, kommen wir auf 10 ⋅ 10 = 100 Möglichkeiten:

Im nächsten Schritt habe ich jene Ergebnisse grün markiert, bei denen die Einerstelle gleich ist, wie die Ziffer für N. Dadurch können wir die Anzahl der Möglichkeiten bereits auf 27 reduzieren:

 

Diese lässt sich noch weiter verringern, denn es gibt zwei Optionen für P, die wir ausschließen können, und zwar 0 und 1, da sonst das Ergebnis der Multiplikation nicht mit der angegebenen Lösung zusammenpassen würde. Eine Multiplikation mit 0 führt nämlich zum einstelligen Ergebnis 0 und eine mit 1 ändert nichts an der Zahl, weshalb sie in diesem Fall fünfstellig bleibt und das Ergebnis außerdem ebenso SIMON sein müsste. Somit bleiben uns noch sechzehn mögliche Fälle:

Als Nächstes können wir den Fall N = 0 ausschließen, weil das Ergebnis NORTON dann in Wirklichkeit nur fünfstellig wäre. Dadurch halbiert sich die Anzahl auf acht Möglichkeiten: 

Wir haben also bei der Multiplikation mit der Einerstelle auf jeden Fall einen Übertrag auf die nächstgrößere Stelle, und zwar entweder 1, 2, 3 oder 4. Ein netter Nebeneffekt dieser Erkenntnis ist, dass wir dadurch gleich O = 0 ausschließen können, weil in diesem Fall die Zehnerstelle der ersten Zahl aufgrund des Übertrags nicht mit jener vom Ergebnis übereinstimmen würde.

Als Nächstes überprüfen wir, bei welchen Multiplikationen die gleiche Ziffer N auf der Einer- und Hunderttausenderstelle beim Ergebnis erzeugt werden kann und können 5 ⋅ 3, 5 ⋅ 5, 6 ⋅ 6 und 8 ⋅ 6 streichen. Das liegt daran, dass der zweite Faktor P in diesen Fällen nicht groß genug dafür ist, denn selbst wenn wir die größtmögliche Ziffer 9 für S und I einsetzen, führen die Ergebnisse 99 ⋅ 3 = 297, 99 ⋅ 5 = 495 und 99 ⋅ 6 = 594 nicht dazu, dass die Ziffer an der Einer- und Hunderttausenderstelle beim Ergebnis gleich ist. Dadurch halbiert sich die Anzahl der Fälle erneut auf vier:

Nun überlegen wir uns, ob wir noch weitere Fälle ausschließen können. Dazu testen wir, welche Zehnerziffern beim ersten Faktor multipliziert mit dem jeweiligen zweiten Faktor (6, 7 oder 9) zusammen mit dem Übertrag von 1 bis 4 wieder zur gleichen Zehnerziffer beim Ergebnis führen:

SIMO2 ⋅ 6 = 2ORTO2
SIMO4 ⋅ 6 = 4ORTO4
SIMO5 ⋅ 7 = 5ORTO5
SIMO5 ⋅ 9 = 5ORTO5

Auf diese Weise können wir für jeden der vier Fälle alle Ziffern von 1 bis 9 für O ausprobieren und sehen, dass der Großteil davon nicht passt. Der einzig verbleibende Fall ist somit 5 ⋅ 9 mit den beiden Möglichkeiten O = 2 und O = 7. Zum Schluss spielen wir einfach alle möglichen Ziffernkombinationen für diese beiden Varianten durch, indem wir die restlichen Stellen mit passenden Ziffern ergänzen:

SIM25 ⋅ 9 = 52RT25
SIM75 ⋅ 9 = 57RT75

Dadurch kommen wir überraschenderweise auf über zwanzig mögliche Lösungen, wobei alle bis auf eine mindestens eine Mehrfachbelegung von Ziffern aufweisen: 

• 57 825 ⋅ 9 = 520 425 (S = N = 5)
• 57 925 ⋅ 9 = 521 325 (S = N = 5 und M = P = 9)
• 58 025 ⋅ 9 = 522 225 (S = N = 5 und O = R = T = 2)
• 58 125 ⋅ 9 = 523 125 (S = N = 5 und M = T = 1)
• 58 225 ⋅ 9 = 524 025 (S = N = 5 und O = M = 2)
• 58 325 ⋅ 9 = 524 925 (S = N = 5 und P = T = 9)
• 58 425 ⋅ 9 = 525 825 (S = N = R = 5 und I = T = 8)
• 58 525 ⋅ 9 = 526 725 (S = M = N = 5)
• 58 625 ⋅ 9 = 527 625 (S = N = 5 und M = T = 6)
• 58 725 ⋅ 9 = 528 525 (S = N = T = 5 und I = R = 8)
• 58 825 ⋅ 9 = 529 425 (S = N = 5 und I = M = 8)
• 63 075 ⋅ 9 = 576 675 (S = R = T = 6)
• 63 375 ⋅ 9 = 570 375 (I = M = R = 3)
• 63 575 ⋅ 9 = 572 175 (M = N = 5)
• 63 675 ⋅ 9 = 573 075 (S = M = 6 und I = R = 3)
• 63 775 ⋅ 9 = 573 975 (M = O = 7 und I = R = 3 und P = T = 9)
• 63 875 ⋅ 9 = 574 875 (M = T = 8)
• 63 975 ⋅ 9 = 575 775 (M = P = 9 und N = R = 5)
• 64 175 ⋅ 9 = 577 575 (O = R = 7 und N = T = 5)
• 64 275 ⋅ 9 = 578 475 (I = R = 4)
• 64 375 ⋅ 9 = 577 375 (O = R = 7 und M = T = 3)

Ich nehme an, dass der Hinweis auf nur zwei mögliche Lösungen um ein zusätzliches Kriterium ergänzt werden sollte: jede Ziffer darf nur einem Buchstaben zugeordnet werden. Die dementsprechend einzige gültige Lösung lautet 63 475 ⋅ 9 = 571 275 mit folgender Belegung: I = 3, M = 4, N = 5, O = 7, P = 9, R = 1, S = 6 sowie T = 2.

Ich bin eigentlich davon ausgegangen, dass ich alle Möglichkeiten berücksichtigt habe und dementsprechend auch zwei Lösungen ohne Mehrfachbelegungen erhalten hätte müssen, aber leider scheint es noch eine andere zu geben. Da ich jedoch keine Lust habe alles noch einmal von vorne durchzugehen, werde ich versuchen, ein Programm zu schreiben, das diese Arbeit für mich übernimmt.

Johannes C. Huber (möchte gerne ein ähnliches Rästel mit seinem eigenen Namen erstellen)

Gamification von Hausarbeit

Thema: To-Do-Listen und Wahrscheinlichkeiten

Manchmal steht ein Punkt auf meiner To-Do-Liste, den ich eigentlich dringend erledigen sollte, obwohl ich partout keine Lust darauf habe. Unter Umständen habe ich ihn deshalb schon mehrere Male aufgeschoben und von einer Liste in die nächste übertragen. Ich bin definitiv nicht die einzige Person auf diesem Planeten, die hin und wieder prokrastiniert, aber seit Jahresbeginn fahre ich ganz gut mit folgender Taktik: Anstatt wertvolle mentale Ressourcen zu vergeuden, weil ich entscheiden muss, welcher Aufgabe ich mich als nächstes widme, überlasse ich das einfach dem Zufall. Deshalb nutze ich seit geraumer Zeit ein virtuelles Glücksrad, um mir die Wahl der Qual abzunehmen.

Diese Idee ist mir gekommen, als ich einem Youtuber bei einem besonders herausfordernden Playthrough von Hitman zugesehen habe. Abgesehen davon, dass er das Spiel auf der höchsten Schwierigkeitsstufe absolviert hat, musste er zusätzlich dazu nach jeweils fünf Minuten Spielzeit ein Glücksrad der Website Picker Wheel drehen. Das Resultat der Drehung konnte eine zusätzliche Aufgabe sein, die er erfüllen musste oder eine selbst auferlegte Einschränkung, an die er sich halten musste. Selbstverständlich würde es mit jedem weiteren Dreh immer schwieriger werden ein Level erfolgreich zu beenden.  

Mein Ziel war natürlich nicht, mir das Leben künstlich zu erschweren. Ganz im Gegenteil. Also habe ich es einfach ausprobiert, um zu sehen, ob ich mich damit selbst in Richtung mehr Effizienz tricksen kann. Ich wurde tatsächlich positiv überrascht, weil ich mit relativ wenig Aufwand gleich viel konsequenter geworden bin. Das liegt unter anderem daran, dass ich das Rad erst wieder drehen darf, wenn die aktuelle Aufgabe abgeschlossen ist. So gerate ich nicht in Versuchung stattdessen irgendwelche potentiell unwichtigeren Tätigkeiten vorzuziehen, um mir selbst Produktivität vorzugaukeln.

Eine Vorgehensweise wie diese ist höchstwahrscheinlich nichts Neues, aber sie macht mir wesentlich mehr Spaß, weil ich erstens nicht mehr selbst aussuchen muss, was als Nächstes drankommt und mich zweitens auch nicht mehr selbst dafür verfluchen kann. So schaffe ich es meist alles zu erledigen, was ich mir für einen Tag vorgenommen habe, weil ich nicht mehr auf potentiell entspanntere Aufgabeb ausweichen kann. Ich würde allerdings anmerken, dass es durchaus ein paar Dinge gibt, die man dabei beachten sollte.

beispielhaftes Glücksrad (Bildquelle: Picker-Wheel) 

Es gibt verschiedene Prinzipien mit stimmig klingenden Abkürzungen, die bei der Formulierung von Zielen helfen können, wie beispielsweise METER (messbar-einfach-terminiert-erreichbar-relevant) oder SMART (spezifisch-messbar-ausführbar-realistisch-terminiert). Abgesehen davon, dass man sie sich leicht merken kann, haben sie durchaus ihre Berechtigung. Daher möchte ich zum Schluss noch ein paar Tipps für die Umsetzung geben.

Die Glücksrad-Methode eignet sich, meines Erachtens, nur für Aufgaben, die sich innerhalb eines Tages erledigen lassen. Die Deadline ist dadurch zwar klar vorgegeben, aber ich empfehle generell nur Aufgaben einzutragen, die nicht allzu viel Zeit in Anspruch nehmen. Ein Eintrag wie "Wohnung putzen" ist wahrscheinlich ein wenig überladen (es sei denn man bewohnt nur ein Zimmer). Als grober Richtwert sollte jede Aufgabe nicht länger als eine Stunde dauern. Falls eine Aufgabe zu zeitintensiv erscheint, lässt sie sich möglicherweise in kleinere Teilaufgaben zerlegen.

Abgesehen davon sollten die Aufgaben am jeweiligen Tag auch tatsächlich erledigt werden können. Es bringt beispielsweise nichts, wenn man an einem Sonntag telefonisch einen Arzttermin vereinbaren möchte, aber die Praxis nicht geöffnet hat und daher niemand abhebt. Außerdem sollten sie voneinander unabhängig sein. Falls man z. B. die beiden Aufgaben "Farbe kaufen" und "Wand streichen" auf der Liste hat, ist die Reihenfolge prädeterminiert und kann nicht dem Zufall überlassen werden.

Bei To-Do-Listen im Allgemeinen ist es hilfreich, die Einträge zumindest halbwegs präzise zu formulieren, damit auch klar ist, was letztlich gemacht werden soll. Man könnte z. B. "Wohnzimmerboden nass wischen" statt einfach nur "Wohnzimmer putzen" schreiben oder "Batterien beim Diskonter kaufen" statt "Einkäufe erledigen".

Um nicht nur Aufgaben in Aussicht zu haben, auf die man wenig Lust hat, kann man auch solche einstreuen, die Freude machen bzw. einen gewissen Ausgleich schaffen, wie beispielsweise ein Kapitel eines Buches zu lesen, das schon seit längerem unangetastet herumliegt oder einen Film schauen, den man sich notiert hat. Das verleiht dem ganzen ein bisschen mehr Glücksspielcharakter, weil man auch auf etwas hoffen kann, das potentiell Spaß macht.

Ich habe ursprünglich mit dem Gedanken gespielt, Felder hinzuzufügen, die z. B. ein erneutes Drehen erlauben, falls man etwas erwischt hat, das man eigentlich lieber später machen möchte. Allerdings würde ich eher davon abraten, weil es den Sinn der Methode zunichte macht, wenn man sich im Endeffekt erst recht wieder vor Aufgaben drücken kann. Es könnte aber durchaus sinnvoll sein dringenden Aufgaben mehr bzw. größere Felder zu geben, damit diese mit einer höheren Wahrscheinlichkeit getroffen werden.

Eine andere Variante ist, stattdessen das Rad einfach laufend mit neuen Aufgaben zu füllen, d. h. auch dann, wenn noch welche übrig sind. Dadurch eröffnet sich zwar die Möglichkeit, unliebsame Aufgaben hinauszuzögern, aber auf kurz oder lang wird jede Aufgabe trotzdem irgendwann einmal dran kommen.

Wer das Gefühl mag, stolz einen Bullet Point nach dem anderen durchzustreichen, sollte es unbedingt einmal ausprobieren. Auch wenn man alle Einträge selbst geschrieben hat, tritt immer noch ein kleiner Überrauschungseffekt auf, sobald sich zeigt, was man erwischt hat. Ich bin jedenfalls hellauf begeistert davon und schreibe seitdem einfach alle Einträge meiner To-Do-Liste in die Felder auf dem Rad und um den Rest kümmert sich der Pfeil.

Johannes C. Huber (hat vom Glücksrad den Auftrag bekommen, endlich diesen Beitrag fertigzustellen)

Hier ein paar weitere Websites mit virtuellen Glücksrädern:

• SpintheWheel.app
• WheelofNames.com
• WheelDecide.com
• Fortunewheel.com