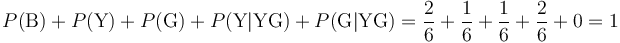Thema: Lego und Wahrscheinlichkeitsrechnung
Ich habe vor etlichen Jahren das Lego-Spiel Banana-Balance geschenkt bekommen. Ziel des Spiels ist, die meisten Bananen von einer Palme zu ernten, ohne dass diese umfällt. In diesem Beitrag geht es allerdings nur um den zugehörigen Spielwürfel. Dieser hat sechs Seiten mit folgenden Motiven:
- 2x braun: der Affe wird auf die Palme gehängt und ggf. werden Bananen geerntet
- 1x gelb: eine weitere Banane wird auf die Palme gesteckt
- 1x grün: ein weiteres Palmenblatt wird auf die Palme gesteckt
- 2x gelb-grün: freie Wahl zwischen den Aktionen von gelb und grün
Wie hoch ist die Wahrscheinlichkeit gelb zu würfeln bzw. eine Banane auf die Palme zu stecken? Wir gehen davon aus, dass jede Seite mit derselben Wahrscheinlichkeit von einem Sechstel gewürfelt wird. Da wir ein gelbes Feld und zwei gelb-grüne haben, kommen wir so auf die Wahrscheinlichkeit ein Halbes bzw. 50 %. Dieselbe Überlegung würde dann auch für grün gelten. Wenn wir die Wahrscheinlichkeiten für die drei Farben addieren, kommen wir allerdings auf vier Drittel bzw. über 100 %. In Summe müsste jedoch 1 heraus kommen, weil mehr als das sogenannte sichere Ereignis nicht möglich ist. Was ist hier schief gelaufen?
Dem geübten Lesepublikum dürfte gleich auffallen, dass die gelb-grünen Felder eigentlich eine eigene Farbe darstellen und daher separat gezählt werden müssen. So kommen wir in Summe* auf ein Ganzes und die Gesetze der Wahrscheinlichkeitsrechnung werden nicht verletzt:
Wie kommen wir nun auf die Wahrscheinlichkeit dafür eine Banane auf die Palme zu stecken? Dazu gehen wir davon aus, dass wir uns auf jeden Fall für gelb entscheiden werden, wenn wir die Wahl haben und kommen damit tatsächlich auf eine Wahrscheinlichkeit von 50 %:
Würden wir das nicht tun und die Wahl einem weiteren Zufallsexperiment überlassen, dann gibt es wiederum eine gewisse Wahrscheinlichkeit um bei gelb-grün auf gelb zu kommen. Falls wir das z. B. mit einem Münzwurf entscheiden, beträgt die Wahrscheinlichkeit dafür gelb zu würfeln nur ein Drittel:
Diese beiden Überlegungen sind im Einklang mit den Gesetzen der Wahrscheinlichkeitsrechnung, aber wo lag vorher das Problem? Um das zu verstehen, müssen wir zwischen Ergebnissen und Ereignissen des Zufallsexperiments unterscheiden. Gelb zu würfeln ist nämlich nicht dasselbe, wie eine Banane aufzuhängen, weil es neben der einzelnen gelben Würfelseite auch noch zwei andere Ergebnisse (sogenannte Elementarereignisse) gibt, bei denen dieses Ereignis eintreten kann, und zwar die beiden gelb-grün gefärbten. Ein Ergebnis ist eben nur ein möglicher Ausgang des Zufallsexperiments. Ein Ereignis wiederum kann auch bei unterschiedlichen Ergebnissen eintreten. Die gelbe Seite zu würfeln bedeutet in diesem Fall also wirklich nur das, während die Banane auch bei zwei anderen Würfelseiten aufgehängt werden kann.
Johannes C. Huber (hat das Spiel noch nie zu Ende gespielt)
* B...braun, Y...Gelb, G...Grün, YG...Gelb-Grün
Quellen: