Thema: Geheimschriften und Permutationen
Im Laufe des Jahres führen wir mit den Wichteln und Wölflingen meiner Gruppe gewisse Aktivitäten durch, die wir als "Pfaditechnik" bezeichnen. Manche Leute denken bei diesem Begriff vielleicht an Bodenzeichen oder Seilknoten und würden damit auch richtig liegen. Ein weiterer typischer Programmpunkt ist das Erlernen von Geheimschriften. Davon gibt es viele bekannte Ableger wie z. B. den Morse-Code oder die Cäsar-Verschlüsselung. Unseren Kindern zeigen wir zu Beginn aber meist einfachere Schriften wie z. B. gespiegelte Buchstaben, Zahlenfolgen oder die Rückwärtsschrift.
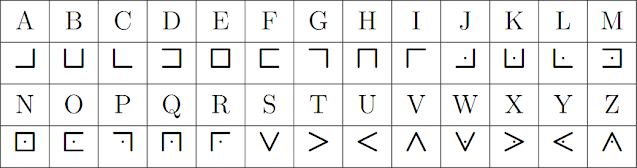
Dieser allgemein als Freimaurer-Chiffre (engl. pigpen cipher) bekannte Gittercode basiert auf einem Verschlüsselungsverfahren, das monoalphabetische Substitution genannt wird, weil dabei einzig die Buchstaben des regulären Alphabets durch andere Zeichen ersetzt werden. Die Umlaute Ä, Ö und Ü müssen in der Regel als AE, OE und UE umgeschrieben werden und das ß entweder als SS oder besser SZ. Manchmal werden aber auch einfach die Doppelpunkte der Umlaute über den Buchstaben beibehalten, wie z. B. in der LaTeX-Version (\usepackage{pigpen}):
hier als Beispiel das Wort "Lösshügelländer" oben mit und unten ohne Umlaute
Das hat allerdings den Nachteil, dass das Entziffern der Geheimbotschaft erheblich vereinfacht wird. Hier fällt uns außerdem ein weiterer Schwachpunkt einer solchen Verschlüsselung auf: zwei gleiche Zeichen hintereinander sind ebenso verdächtig. In deutschen Texten stehen sie meist für SS und können daher unter Umständen recht einfach zugeordnet werden. Nun aber zurück zu einem anderen Problem dieser Geheimschrift: Es gibt kein einheitliches Zeichenset für den Schlüssel sondern etliche verschiedene Versionen.
Der erste Unterschied liegt in der Bildung der Buchstabenpaare. Ich habe festgestellt, dass i. A. drei verschiedene Varianten zum Einsatz kommen:
Diese kommt beispielsweise bei der entsprechenden Schriftart in Microsoft Word zum Einsatz.
2) Bei der Standard-Variante werden erst die Zellen des 3x3-Rasters und danach die des Kreuzes in jeweils zwei Durchgängen (also ##XX) mit Buchstaben gefüllt:
Diese entspricht dem Zeichensatz, der im LaTeX-Paket enthalten ist.
3) Bei der traditionellen Variante (US-amerikanisches System) werden die Zellen der beiden Raster nacheinander in zwei Durchgängen (also #X#X) mit Buchstaben gefüllt:
Der Schlüssel der englischen Variante ist, meiner Meinung nach, ein wenig intuitiver als jener der anderen beiden. Falls man weder den Schlüssel, noch etwas zum Schreiben zur Hand hat, reicht es aus sich die 13 Zeichen ohne Punkt zu merken und von dort jeweils für den darauffolgenden Buchstaben weiterzurücken.
Der zweite Unterschied hängt mit der Leserichtung in den Gitterzellen zusammen. Grundsätzlich wird immer zuerst das 3x3-Raster durchlaufen und danach das Kreuz, aber es scheint eine gewisse Willkür bei der Anordnung der Buchstabenpaare im zweiten Raster zu geben.
In den meisten Zeichensätzen, die ich gefunden habe, wird ganz normal von links nach rechts und von oben nach unten gelesen. Das bedeutet, dass wir auch im Kreuz oben beginnen, danach die linke Seite, gefolgt von der rechten lesen und zum Schluss im unteren Feld landen. Ich persönlich bezeichne diese Leserichtung als Blitz, weil sie mich an das Widerspruch-Symbol aus der Mathematik erinnert. In manchen Fällen werden die Felder beim Kreuz jedoch stattdessen im bzw. gegen den Uhrzeigersinn oder gar versetzt gelesen:
Wie viele verschiedene Schlüssel sind insgesamt möglich?
Zunächst klingt es vielleicht so, als ob wir dazu herausfinden müssten, wie viele verschiedene Sets von 13 Buchstabenpaaren wir bilden können. Da die Buchstaben alle unterscheidbar sind, handelt es sich dabei um eine Art Ziehen ohne Zurücklegen. Es gibt 26 über 2 Möglichkeiten für das erste Buchstabenpaar, 24 über 2 für das zweite und so weiter. Wir kommen so auf eine Verkettung von insgesamt dreizehn Binomialkoeffizienten und erhalten folgendes Ergebnis:
Das sind bereits mehrere Trilliarden Möglichkeiten, aber es gibt noch ein kleines Problem: Wir unterscheiden hier nicht zwischen Paaren wie z. B. AB und BA. In anderen Worten: Es ist nicht eindeutig, welcher Buchstabe dabei welches Zeichen der Geheimschrift belegt. Die Reihenfolge der Buchstaben in den beiden Rastern spielt aber durchaus eine Rolle. Wir müssen diesen Umstand also irgendwie berücksichtigen.
Da alle Elemente unserer Grundmenge (das Alphabet) relevant sind, ist es nötig stattdessen die Anzahl aller möglichen Anordnungen (die sogenannten Permutationen) bestimmen. Wir suchen also alle Möglichkeiten um die 26 Buchstaben als Paare in die 13 Zellen zu schreiben. Es scheint zwar so, als ob die Bildung der Paare eine Rolle spielt, aber eigentlich interessiert uns dabei nur, welcher Buchstabe an welchen der 26 Plätze kommt. Das geübte Lesepublikum weiß, dass wir es hier mit einer Fakultät zu tun haben:
Damit kommen wir sogar auf mehrere Quatrillionen mögliche Schlüssel für den Gittercode. Glücklicherweise sind nur relativ wenige davon intuitiv und somit brauchbar. Wir schränken die Auswahl nun auf jene Paarbildungen ein, die uns sinnvoll erscheinen: die drei oben beschriebenen Arten der Einteilung (Standard, UK und US). Wir bilden also drei Mengen für die Buchstabenpaare, die wir wiederum in jeweils zwei Teilmengen für die beiden unterschiedlichen Raster unterteilen:
Im nächsten Schritt beziehen wir nur noch die gängigen Leserichtungen mit ein. Für die jeweils erste Teilmenge der beiden Varianten (also das 3x3-Raster) gibt es nur eine Möglichkeit für die Anordnung, wenn wir voraussetzen, dass hier immer von links nach rechts und oben nach unten gelesen wird. Ich habe bisher jedenfalls keinen Schlüssel gefunden, bei dem das 3x3-Raster eine andere Leserichtung aufweist. Beim zweiten Raster gibt es wiederum vier verschiedene Leserichtungen bzw. vier verschiedene Anordnungen für die Elemente der jeweils zweiten Teilmenge. Damit kommen wir in Summe auf immerhin zwölf mögliche Varianten für die Schlüssel. Ich habe hier die neun Permutationen zusätzlich zur Blitzleserichtung veranschaulicht:
Wir sollten uns also nicht wundern, wenn eine andere Person Probleme damit hat unsere Geheimbotschaften zu entziffern, weil die Wahl des vermeintlich richtigen Schlüssels eben davon abhängt, welches System und welche Leserichtung man kennt.
Der Gittercode ist generell keine sichere Geheimschrift, aber wir können das Entschlüsseln zumindest ein wenig erschweren, indem wir verschiedene Schlüssel miteinander kombinieren. Dazu übersetzen wir zuerst unsere Geheimbotschaft mit einem Schlüssel in die Schriftzeichen und dann mit einem anderen Schlüssel zurück in deutsche Buchstaben. Diesen Schritt können wir theoretisch beliebig oft wiederholen. Der dadurch entstandene Text hat mit ziemlicher Sicherheit keinerlei Bedeutung mehr und kann nur dann problemlos dechiffriert werden, wenn man sowohl die verwendeten Schlüssel, als auch ihre Reihenfolge kennt.
Gewisse Schwachstellen verschwinden jedoch auch in diesem Fall nicht. Neben doppelten Buchstaben und den Häufigkeiten bestimmter Zeichen in der deutschen Sprache können wir auch den Umstand nutzen, dass der Buchstabe A in allen gängigen Varianten demselben Zeichen entspricht, um den Code zu knacken.
Johannes C. Huber (ihnkqiofu jqeou, elgis zw dlhcqjqirij)
An dieser Stelle ein herzliches Dankeschön für wertvollen fachlichen Input von Stefan!
Quellen:
- Dorfmayr A. (2007): Von Cäsar bis RSA
- Beitrag des Tiroler Bildungsservice mit der Standard-Variante
- Liste mit allen offiziellen Varianten
- Freimaurer-Alphabet-Entschlüssler
- Programm der Gruppe Wien 55 für die UK-Variante mit Leserichtung im Uhrzeigersinn
- Geheimschriften-Sammlung der Jungschar mit Standard-Variante und Abwandlungen
- UK-Variante der Gruppe Zeiselmauer mit abgewandelter Leserichtung
- Generator der Gruppe Linz 2 für die UK-Variante mit abgewandelter Leserichtung
PS: Abgesehen von diesem Gittercode gibt es auch noch einen anderen, dessen Schlüssel mit nur einem 3x3-Raster auskommt. Dieses wird dabei nicht mit Paaren, sondern Tripeln von Buchstaben gefüllt und enthält als 27. Zeichen ein weiteres E:
Das hängt vermutlich damit zusammen, dass der Buchstabe E in deutschsprachigen Texten mit Abstand am häufigsten vorkommt (17,4%) und so verhindern soll, dass die Geheimbotschaft deswegen zu einfach entziffert werden kann. Auch hier sind Abwandlungen möglich: