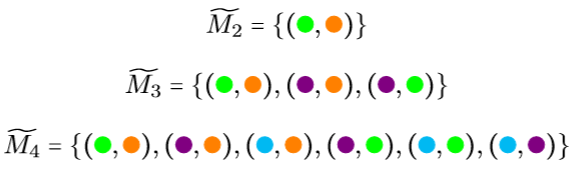Zwei Paar Schuhe sind drei Paar Schuhe

Thema: Schuhe und Kombinatorik

Der Sager ”Zwei Paar Schuhe sind drei Paar Schuhe.” meint im Wesentlichen, dass Fußbekleidung länger hält, wenn sie nicht jeden Tag getragen wird. Das ist insbesondere bei Lederschuhen der Fall, weil die beim Tragen entstandene Feuchtigkeit danach erst wieder verdunsten muss. Zwei Paar Schuhe, die abwechselnd getragen werden, haben demnach eine gleich lange Lebensdauer, wie drei Paar Schuhe, die jeden Tag getragen werden. In anderen Worten: ein Paar Schuhe überlebt eineinhalbmal so lange, wenn es nur jeden zweiten Tag getragen wird.

Diese Vorgehensweise sollte allerdings Hausverstand sein und wie lange ein Paar Schuhe nun im Schnitt tatsächlich hält, interessiert vermutlich vor allem Unternehmen, die Schuhe produzieren. Mathematisch interessant wird es, wenn wir uns überlegen, was passiert wenn verschiedene Schuhe miteinander kombiniert werden. Dafür nehmen wir es allerdings wortwörtlich.

Von zwei linken Füßen... 

Wie wäre es, wenn wir die Aussage so interpretieren, dass damit gemeint ist, wie viele verschiedene Paare, wir aus einer bestimmten Anzahl von Ausgangspaaren (in diesem Fall zwei) zusammenstellen können? Der Einfachheit halber kümmern wir uns vorerst einmal nicht darum, welcher Schuh auf welchem Fuß landet. Ein gutes Beispiel für derartiges Schuhwerk sind übrigens einfache Hausschuhe aus Stoff oder Filz, weil sie teilweise so einheitlich gefertigt werden, dass es keine Rolle spielt ob nun der rechte oder linke Fuß darin steckt (siehe Bild). Bei den meisten Socken ist es übrigens ähnlich.

 einheitlich gefertigte Pantoffeln (Bildquelle: Pixy)

Angenommen wir haben zwei verschiedenfarbige Paar Hausschuhe (z. B. ein oranges und ein grünes) und möchten wissen, wie viele verschiedene Kombinationen wir mit einer bestimmten Anzahl von Schuhpaaren machen können ohne dabei auf die Füße zu achten. Für ein Paar ist das trivialerweise 1, weil wir ja insgesamt nur zwei Schuhe zur Verfügung haben und es egal ist, welcher davon links oder rechts getragen wird. Wir nennen die Menge möglicher Kombinationen ab jetzt M_i, wobei i die Anzahl der Paare beschreibt, die uns zur Verfügung stehen. |M_i| beschreibt die Größe (Mächtigkeit) dieser Menge, also die Anzahl ihrer Elemente. Für ein Paar (i = 1) erhalten wir:

Für zwei, drei und vier Paare können wir die möglichen Kombinationen noch ohne allzu viel Aufwand der Reihe nach durchgehen und auch relativ kompakt notieren: 

Wir stellen fest, dass das Sprichwort auch in diesem Fall stimmt, denn zwei Paar Schuhe (Elemente) sind tatsächlich drei Paar Schuhe (Kombinationen). Drei Paar Schuhe wiederum ermöglichen sechs Kombinationen und vier sogar schon zehn, aber für fünf oder mehr Paare wird diese Darstellungsform leider recht schnell sehr unübersichtlich. Wir müssen uns deshalb eine andere Methode überlegen, wie wir die Anzahl der möglichen Kombinationen auf einfachere Art und Weise erhalten. 

Nun kommt die Kombinatorik ins Spiel. Die Frage ist, wie viele verschiedene Paare ich aus der Menge der Schuhe ziehen kann, d. h. wie viele verschiedene 2-elementige Mengen ich mit den Elementen der Menge der Schuhe bilden kann. Diese Formulierung legt nahe mit dem Binomialkoeffizienten zu arbeiten, aber ganz so einfach ist das leider nicht. Für ein Paar erhalten wir zwar das richtige Ergebnis, aber ab zwei Paaren stimmen die Werte nicht mehr, weil dabei nicht berücksichtigt wird, dass wir nicht zwischen den gleichfarbigen Schuhen unterscheiden:

\[\binom{2}{2} = 1 \quad \checkmark \qquad \binom{4}{2} = 6 \quad \times\]

\[\binom{6}{2} = 15 \quad \times \qquad \binom{8}{2} = 28 \quad \times\]

Da wir Kombinationen mit zwei linken oder rechten Schuhen zulassen funktioniert dieses Konzept nicht. Glücklicherweise gibt es eine geeignete Vorgehensweise, aber dafür müssen wir uns etwas geringfügig anderes vorstellen: Angenommen wir haben keine Schuhpaare vor uns, sondern ein Art ”Schuhautomat”, aus dem wir nacheinander zwei Schuhe ziehen, d. h. es gibt eine bestimmte Anzahl an unterschiedlichen Optionen aus denen wir auswählen können. Das Ganze funktioniert also genau so wie bei einem Getränke- oder Snackautomaten, nur eben mit Schuhen. Es könnte z. B. sein, dass es sich zwar bei allen Schuhen um dasselbe Modell handelt, allerdings in unterschiedlichen Farben. Auf diese Art können wir den Vorgang als Ziehen mit Zurücklegen interpretieren, wobei uns die Reihenfolge egal ist, weil es ja, wie gesagt, keine Rolle spielt, auf welchen Fuß ein Schuh kommt. Wir verwenden folgende Formel, wobei n für die Anzahl der Optionen und k für die Anzahlder ausgewählten Schuhe steht:

\[\binom{n+k-1}{k} \quad \text{bzw.} \quad \binom{n+k-1}{n-1}\]

In diesem Fall ist k stets 2 (außer wir überlegen uns das Ganze für Lebewesen, die mehr als zwei Füße haben und Schuhe tragen). Wir setzen probeweise die Werte für ein bis vier Paare ein und stellen fest, dass die Formel das gewünschte Ergebnis liefert:

\[\binom{2}{0} = 1 \quad \checkmark \qquad \binom{3}{1} = 3 \quad \checkmark\]

\[\binom{4}{2} = 6 \quad \checkmark \qquad \binom{5}{3} = 10 \quad \checkmark\]

Dadurch werden alle Möglichkeiten für den ersten Schuh mit allen Möglichkeiten für den zweiten Schuh gezählt, ohne dass bereits vorgekommene Kombinationen erneut gezählt werden. Wir haben also eine allgemeingültige Formel für die Anzahl der möglichen Kombinationen gefunden:

\[|M_n| = \binom{n+1}{2} = \binom{n+1}{n-1}\]

...über modische Feinheiten...

Die Aussage stimmt, wenn wir alle möglichen Kombinationen der Ausgangspaare betrachten, aber wie sieht es mit Variationen aus? Das geübte Lesepublikum wird bereits erahnen, wie die Antwort lautet. Das bedeutet nämlich, dass es ab jetzt sehr wohl darauf ankommt, ob z. B. bei der Kombination orange-grün der grüne Schuh links oder rechts getragen wird. Variationen bringen nämlich nichts wirklich Neues, sondern erweitern nur die Optionen. 

Fangen wir wieder mit einem einzelnen Paar an und geben nun vor, dass ein Schuh für den rechten und einer für den linken gemacht ist. Eine Möglichkeit das zu notieren wäre vielleicht so etwas in diese Richtung: (L, R). Das ist jedoch gar nicht nötig. Wir überlegen uns stattdessen einfach, ob es zusätzlich zu den bisherigen Paarbildungen überhaupt noch weitere gibt, wenn es nun doch einen Unterschied macht, welche Farbe zuerst kommt. Der Vollständigkeit halber sei an dieser Stelle angemerkt, dass es keinen Unterschied macht, wenn gleichfarbige Schuhe die Plätze tauschen. Bei einem Paar sind deshalb alle Möglichkeiten bereits ausgeschöpft, aber bei zwei Paaren kommt so noch eine vierte hinzu und zwar die Spiegelung der gemischten Farbkombination. Bei drei Paaren gibt es drei und bei vier Paaren sogar sechs weitere Möglichkeiten. Die komplementären Mengen für zwei bis vier Paare können wir aufschreiben indem wir einfach jede Kombination unterschiedlicher Farben spiegeln:

Ich werde nun den Umstand, dass linke Schuhe nur auf linke Füße passen und umgekehrt, nutzen um die Methode zu erläutern, mit der wir die Anzahl der Variationen bestimmen können. Wir betrachten den Stapel mit linken Schuhen getrennt von jenem mit den rechten Schuhen und gehen o. B. d. A. davon aus, dass wir zuerst einen linken Schuh anziehen. Bei zwei Paaren haben wir zwei Möglichkeiten für den linken Fuß. Danach ziehen wir einen rechten Schuh an und haben wieder zwei Möglichkeiten: 2 ⋅ 2 = 4. Dasselbe Spiel lässt sich für drei (3 ⋅ 3 = 9) und vier Paare (4 ⋅ 4 = 16) wiederholen. Uns fällt auf, dass das Ergebnis dadurch ganz einfach stets das Quadrat der Anzahl der Paare ist, was an der Formel der Variationen für Ziehen mit Zurücklegen liegt:

\[|M_n| = \binom{n}{k} \text{ (wobei } k \text{ in diesem Fall immer gleich } 2 \text{ ist)}\]  

Das bedeutet, dass wir z. B. mit nur zehn verschiedenen Paar Schuhen, theoretisch hundert Tage hintereinander jedes Mal ein anderes ”Paar” tragen können. Vorausgesetzt es stört uns nicht, dass die meisten Looks zweimal vorkommen.  

...bis hin zur Kunst in den falschen Schuh zu schlüpfen.

Dass der Platztausch gleichfarbiger Schuhe nicht gezählt wurde, können wir auch damit begründen, dass linke Schuhe nicht auf rechte Füße passen und umgekehrt. Die zusätzlichen Möglichkeiten, die wir vorher nicht gezählt haben, sind also einfach nur die gespiegelten Variationen. Was wäre, wenn wir nun aber doch zulassen, dass linke Füße in rechte Schuhe schlüpfen können und umgekehrt? Die Antwort ist simpel: Da es sich um eine Spiegelung der Variationen handelt, verdoppeln wir einfach die Anzahl der Möglichkeiten. Ungeachtet dessen, dass die Hälfte davon dadurch vermutlich ziemlich unbequem sind (es sei denn es handelt sich um billige Gästepantoffeln).

Wer barfuß geht, den drücken die Schuhe nicht. 

Selbstverständlich können wir auch noch den Fall 0 betrachten. Das bedeutet nicht anderes als kein Paar Schuhe, also barfuß und dürfte das womöglich langlebigste Paar sein, das man haben kann. Was die modische Flexibilität betrifft, sind sie natürlich nicht annähernd so wandlungsfähig wie echte Fußbekleidung, aber Tatsache ist, dass es eben darauf ankommt, wie die Aussage interpretiert wird, denn Kombinationen und Variationen sind und bleiben zwei Paar Schuhe.

Johannes C. Huber (wird seine Schuhe höchstwahrscheinlich auch weiterhin nicht kombinieren)

PS: Es wäre sicherlich interessant den Fall für Lebewesen mit mehr als zwei Füßen zu betrachten.Vor allem wenn man neben links und recht noch weitere unterschiedliche Seiten betrachtet oder mehrere linke und rechte.