Wann läutet es, Herr Professor?

Thema: Wanduhren und Schulmathematik

Mit Beginn dieses Schuljahres habe ich den nächsten Schritt auf der schulischen Karrierleiter gewagt und darf nun als Klassenvorstand eine erste Klasse begleiten. Zu den vielen Aufgaben, die nicht dezidiert in meiner Jobbeschreibung stehen, zähle ich auch das Einrichten des Klassenraums. Da wir keine Uhr hatten, habe ich das als Anlass genommen, endlich eine von den unzähligen "mathematischen" zu besorgen:

Klassenuhr Version 1.0 (Bildquelle: Johannes C. Huber)

Dekoelemente wie diese wecken im Idealfall gleich unsere Neugier à la "Ich weiß, dass an dieser Stelle jene Zahl stehen muss, aber warum?". Es gibt unzählige solche Ziffernblätter mit unterschiedlicher Komplexität im Internet zu finden. Ich habe mich für diese Variante entschieden, weil sie eine ausgewogene Mischung an Teilbereichen abdeckt und außerdem, meiner Meinung nach, einen gutes Mittelmaß zwischen einfacher und höherer Mathematik darstellt.

Ziffernblatt der Uhr (Bildquelle: Johannes C. Huber)

Die meisten Einträge auf der Uhr lassen sich mit Mathematik aus dem Schulstoff beantworten. Allerdings gehen manche davon ein wenig über die üblichen Themenbereiche hinaus:

• 1 (11. Schulstufe): Dazu müssen wir die sogenannte Eulersche Identität kennen:
  

  
  

  Aus der Gleichung ergibt sich, dass die Eulersche Zahl e hoch die Kreizahl Pi mal die imaginäre Einheit i die Zahl -1 ergibt. Die Gegenzahl dieses Ausdrucks ist somit 1.
  
• 2 (10. Schulstufe): Hier haben wir es mit einer unendlichen geometrischen Reihe zu tun. Das Sigma steht für eine Summe. Rechts davon steht der Term, der uns sagt, wie die Glieder der Reihe bzw. die Summanden beschaffen sind. Diese werden laufend zusammengezählt. Die Laufvariable i unter dem Sigma legt den Startpunkt (hier die Zahl 0) fest und die Lemniskate darüber bedeutet, dass wir diesen Prozess, zumindest theoretisch, unendlich lange fortsetzen. Das erste Glied der Reihe ergibt ein Ganzes, das zweite ein Halbes, das dritte ein Viertel, das vierte ein Achtel und so weiter. Die Zwischensumme wächst zwar immer weiter an, aber auch mit jedem Summand nur mehr halb so viel wie davor. Die ersten paar Zwischensummen lauten 1 - 1,5 - 1,75 - 1,875 - ... Der Grenzwert der Reihe, gegen die sie strebt, ist 2. Diesen Umstand können wir uns auch schön veranschaulichen:
  

  

• 3 (10. Schulstufe): Der natürliche Logarithmus zur Basis e (ln - logarithmus naturalis) der Zahl 21 ist 3,0445224377234229965005979803657... und kaufmännisch abgerundet ungefähr 3.
• 4 (10. Schulstufe): Der Logarithmus zur Basis 10 (lg - logarithmus generalis bzw. dekadischer Logarithmus) der Zahl 10 000, die hier vermutlich aus Platzgründen als Hochzahl geschrieben steht, ist die Zahl 4. Da es sich bei 10 000 um eine Potenz von 10 handelt, können wir stattdessen auch einfach die Anzahl der Nullen zählen.
  
• 5 (7. Schulstufe): Hier sehen wir das kleinste nichttriviale* pythagoräische Tripel als rechtwinkliges Dreieck mit den beiden Kathetenlängen 3 und 4 veranschaulicht. Dabei handelt es sich um drei ganze Zahlen a, b und c, die zusammen den pythagoräischen Lehrsatz a² + b² = c² erfüllen. Die fehlende Zahl bzw. die Länge der Hypotenuse im Dreieck ist 5, da 3² + 4² = 5².
  
• 6 (11. Schulstufe): Diese Notation steht für eine dreielementige Menge A. Wir sollen die Anzahl der Permutationen, d. h. die Anzahl der verschiedenen Möglichkeiten, um ihre (voneinander unterscheidbaren) Elemente anzuordnen, bestimmen. Das ist in diesem Fall auf 3! = 3 ⋅ 2 ⋅ 1 = 6 verschiedene Arten möglich, da es drei Auswahlmöglichkeiten für das erste Elemente gibt, zwei für das zweite und nur eine für das noch verbleibende. Zur Veranschaulichung: Angenommen die drei Elemente heißen x, y und z, dann lauten die Permutationen xyz, xzy, yxz, yzx, zxy und zyx.
  
• 7 (6. Schulstufe): Hierzu muss man wissen, dass ein Siebtel auch als die Dezimalzahl 0,142857... dargestellt werden kann. Der Kehrwert dieser Zahl ist also 7.
  
• 8 (7. Schulstufe): Die Kubikzahl bzw. dritte Potenz von 2 ist 8.
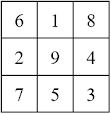
• 9 (5. Schulstufe): Hierbei dürfte es sich um ein sogenanntes magisches Quadrat handeln, in das wir die Zahlen von 1 bis 9 einsetzen müssen, um in jeder Zeile und Spalte die Summe 15 zu erhalten. Damit das auch entlang der Diagonalen funktioniert, müsste die Zahl 5 im Zentrum stehen. Allerdings wissen wir hier bereits, dass dort die 9 stehen muss. In diesem Fall gilt die Summe also nur für die Zeilen und Spalten. Das vollständig ausgefüllte magische Quadrat sieht dann so aus:
  

  

• 10 (6. Schulstufe): 9,999... ist eine andere Darstellung der Zahl 10. Eine Möglichkeit, um diesen Umstand plausibel zu machen, ist die Bruchdarstellung. 0,111... ist ein Neuntel als Dezimalzahl, also muss das Neunfache davon, nämlich 0,999... gleich neun Neuntel bzw. ein Ganzes sein. Somit ist in diesem Fall auch 9 + 0,999... = 9 + 1 = 10.
  
• 11 (7. Schulstufe): Die Quadratwurzel von 121 ist 11**.
  
• 12 (9. Schulstufe): Hierbei handelt es sich um die Zahl 12 in der Zahlendarstellung zur Basis 2 (Binärsystem), da 1 ⋅ 2³ + 1 ⋅ 2² + 0 ⋅ 2¹ + 0 ⋅ 2⁰ = 12.
  

Meine Erstklässler haben mich übrigens gleich damit konfrontiert, dass sie diese Uhr nicht lesen können. Das liegt allerdings nicht an der Beschriftung, sondern ganz einfach daran, dass sie sich noch schwer damit tun, analoge Uhren zu lesen. Ich habe nicht klein bei gegeben, weil es mir wichtig ist, dass sie auch diese Kulturtechnik beherrschen. Als Kompromiss, der hoffentlich auch zur allgemeinen Pünktlichkeit beiträgt, habe ich dann aber die alte Uhr aus meiner Wohngemeinschaft aufgehängt:

Klassenuhr 2.0 (Bildquelle: Johannes C. Huber)

Auf dem Ziffernblatt habe ich den Kindern außerdem die Pausenzeiten in verschiedenen Farben aufgemalt, damit sie besser einschätzen können, wie viel Zeit sie noch haben. Sobald der Minutenzeiger den entsprechenden Kreisringsektor überquert hat, ist die jeweilige Pause vorbei. Bis jetzt funktioniert unser System vergleichsweise gut. Mit etwas Übung dürfte auch das Lesen der analogen Uhr kein Problem mehr darstellen und ich kann wieder eine mathematischere Variante aufhängen.

Herzlichen Dank für wertvollen Input von Sergey und Christina!

Johannes C. Huber (möchte irgendwann auch selbst ein mathematisches Ziffernblatt gestalten)

* Das kleinste triviale Tripel ist 0² + 0² = 0². Andere wären z. B. 1² + 0² = 1² und so weiter.

** An dieser Stelle möchte ich auf eine Fehlvorstellung in Zusammenhang mit dem Wurzelziehen hinweisen. Manchmal wird nämlich behauptet, dass jede reelle Zahl (außer 0) zwei Quadratwurzeln hat. Das hängt damit zusammen, dass wir diesen Sachverhalt als quadratische Gleichung angeben können. In diesem Fall ist neben 11 auch -11 eine Lösung der Gleichung x² = 121, da das negative Vorzeichen durch das Quadrieren verschwindet. So weit so richtig, doch die Quadratwurzel einer Zahl ist eindeutig als nicht negativ definiert. In anderen Worten: Auf die Frage, welche reelle Zahl quadriert werden muss, um eine bestimmte zu erhalten, gibt es (außer bei 0) zwei Antworten, aber auf die Frage, was die Quadratwurzel einer reellen Zahl ist, gibt es nur eine.